Choose r items from n items, allowing repetition, and calculate the total number of ways they can be arranged in order.

Enter the total number (n) and the number selected (r) and click the "Calculate Permutations" button to select r items from the n items, allowing repetition, and calculate and display the total number of ways they can be arranged in order.

It also shows how to calculate the total number of arrangements.

Please enter positive integers up to 10,000 for Total number and Selected number.

A permutation is a sequence of several distinct things chosen and arranged.

The sequence of numbers selected and arranged while allowing repetition is called Permutations with repetition.

For example, let's say you choose two letters from the three letters A, B, and C and arrange them in order.

You can choose the same thing as your first choice, so if you draw the order in a tree diagram, it will look like this:

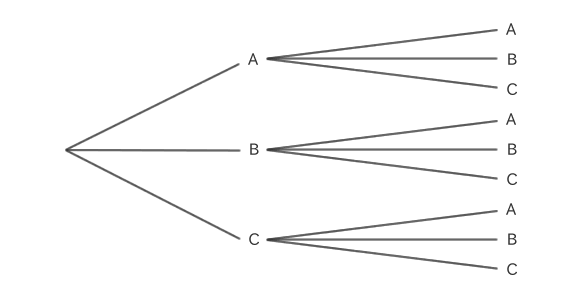
In this case, there are nine possible arrangements: AA, AB, AC, BA, BB, BC, CA, CB, and CC.

When calculating the total number of ways to arrange things in a Permutations with repetition, you can choose the same thing as your first choice, so the number of ways to choose will always be the same as the total number.

For example, suppose there are four letters, A, B, C, and D, and you choose three of them to arrange in order.

The first one has four possibilities: A, B, C, and D, and the second one and beyond have the same four possibilities.

Therefore, the total number of arrangements is 4×4×4, or 64.

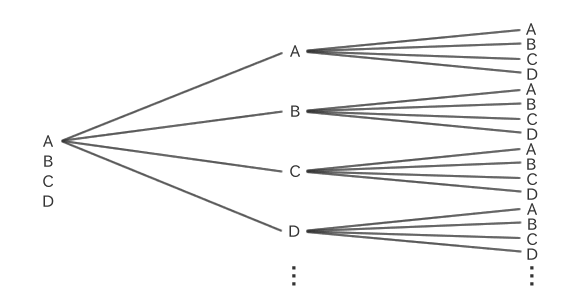
In this way, the total number of ways in which numbers (r) selected from the total number (n) in Permutations with repetition can be arranged is n multiplied by r, since n is the number selected (r).